Sijun He's Unsupervised Learning

Quantization Basics

  • Jun 04, 2023

Quantization Basics

  • Quantization maps a floating point value $x \in [f_{min}, f_{max}]$ to a integer $q \in [q_{min}, q_{max}]$. By performing computations and storing tensors at lower bits, quantization enables a more compact model representation and faster inference on some hardware
  • The most basic quantization is affine quantization, which essentially bins the range of the floating point range with zero point $z$:
\[scale = \frac{f_{max} - f_{min}}{q_{max} - q_{min}}\] \[quant(x) = clamp(round(\frac{x}{scale}) + z, q_{min}, q_{max})\] \[dequant(y) = (y - z) * scale\]
  • the most commonly-used quantization is uniform symmetric affine quantization, with builds on top of afffine quantization with additional constraints such as $z = 0$ and $f_{max} - f_{min} = 2 * absmax(f)$. This simplifies the above formula to:
\[scale = \frac{absmax(f)}{2^{bits - 1}}\] \[quant(x) = clamp(round(\frac{x}{scale}), q_{min}, q_{max})\] \[dequant(y) = y * scale\]

Now let’s try to implement a basic version of the above quantization in numpy:

import numpy as np

class Quantizer:
    def __init__(self, x, bits=8):
        self.qmin = - 2 ** (bits - 1)
        self.qmax = 2 ** (bits - 1) - 1
        self.scale = 2 * np.max(np.abs(x)) / 2 ** bits
        # np has no int4 out-of-the-box so we use int8 here
        self.dtype = np.int8

    def quantize(self, x):
        return np.clip(np.round(x / self.scale), self.qmin, self.qmax).astype(self.dtype)

    def dequantize(self, y):
        return y.astype(np.float32) * self.scale

x = np.random.rand(10, 10).astype(np.float32)
int8_quantizer = Quantizer(x, bits=8)
int4_quantizer = Quantizer(x, bits=4)
int8_diff = x - int8_quantizer.dequantize(int8_quantizer.quantize(x))
int4_diff = x - int4_quantizer.dequantize(int4_quantizer.quantize(x))
print(f"int8 - Max Diff: {np.max(np.abs(int8_diff)):.3e} Avg Diff: {np.mean(np.abs(int8_diff)):.3e}")
print(f"int4 - Max Diff: {np.max(np.abs(int4_diff)):.3e} Avg Diff: {np.mean(np.abs(int4_diff)):.3e}")
# int8 - Max Diff: 7.642e-03 Avg Diff: 2.029e-03
# int4 - Max Diff: 1.223e-01 Avg Diff: 3.313e-02

We see a smaller quantization error when quantizing to int8 than int4, which is expected.

Quantized Matrix Multiplication

Now we know how to represent a tensor in low bits, how do we do matrix multiplication in low bits? Let’s take an example of $XW$, where $X \in \mathcal{R}^{m x n}$ and $W \in \mathcal{R}^{n x k}$. $Q_{X}$ and $Q_{W}$ are the quantized version of $X$ and $W$ respectively.

\[\begin{aligned} Z_{ij} &= \sum_{p=1}^{n} X_{ip} W_{pj} \\ &= \sum_{p=1}^{n} (Q_{X_{ip}} * scale_x) (Q_{W_{pj}} * scale_w) \\ &= scale_x * scale_w \sum_{p=1}^{n} Q_{X_{ip}} Q_{W_{pj}} \\ &= scale_y Q_{Z_{ij}} \end{aligned}\]

Essentially, since the quantization transformation is affine, we can just do the integer matrix multiplication instead of floating point matrix multiplication.

X = np.random.rand(10, 5).astype(np.float32)
W = np.random.rand(5, 4).astype(np.float32)
int8_quantizer_x = Quantizer(X, bits=8)
int8_quantizer_w = Quantizer(W, bits=8)
int_8_X = int8_quantizer_x.quantize(X)
int_8_W = int8_quantizer_w.quantize(W)

fp_32_results = np.matmul(X, W)
int_8_results = np.matmul(int_8_X, int_8_W, dtype=np.int32).astype(np.float32) * int8_quantizer_x.scale * int8_quantizer_w.scale
diff = fp_32_results - int_8_results
print(f"Max Diff: {np.max(np.abs(diff)):.3e} Avg Diff: {np.mean(np.abs(diff)):.3e}")
# Max Diff: 9.942e-03 Avg Diff: 2.976e-03

Quantization Types

Weight-Only Quantization

  • Only weight is statically quantized, activation is not quantized
  • Storing model weights in int8 instead of float32 reduces memory bandwidth. Since computation still happens in fp32, it does not reduce compute bandwidth.
input_fp32 -- linear_int8_w_fp32_inp -- output_fp32
                     /
   linear_weight_int8

num_batches = 5
W = np.random.rand(5, 4).astype(np.float32)
int8_quantizer_w = Quantizer(W, bits=8)
int_8_W = int8_quantizer_w.quantize(W)


for i in range(num_batches):
    X = np.random.rand(10, 5).astype(np.float32)
    fp32_results = np.matmul(X, int_8_W)

Dynamic Quantization

  • weight is statically quantized, activation is quantized on-the-fly with data range observed at runtime
  • Reduces both memory bandwidth and compute bandwith. However, there is extra overhead due to on-the-fly quantization
input_fp32 -- input_int8 -- linear_with_activation_int8 -- if next layer is quantized --Y-- output_int8
                              /                                          \ N
                 linear_weight_int8                                     output_32

num_batches = 5
# W quantized statically
W = np.random.rand(5, 4).astype(np.float32)
int8_quantizer_w = Quantizer(W, bits=8)
int_8_W = int8_quantizer_w.quantize(W)


for i in range(num_batches):
    X = np.random.rand(10, 5).astype(np.float32)
    # X quantized on-the-fly
    int8_quantizer_x = Quantizer(X, bits=8)
    int_8_X = int8_quantizer_x.quantize(X)
    int_8_results = np.matmul(int_8_X, int_8_W, dtype=np.int32)
    if output_fp32:
        fp32_results = int8_quantizer_x.scale * int8_quantizer_w.scale * int_8_results.asdtype(np.float32)

Static Quantization

  • both weight and activations are statically quantized
  • Reduces both memory bandwidth and compute bandwith
input_int8 -- linear_with_activation_int8 -- output_int8
                    /
  linear_weight_int8

num_batches = 5
# W quantized statically
W = np.random.rand(5, 4).astype(np.float32)
int8_quantizer_w = Quantizer(W, bits=8)
int_8_W = int8_quantizer_w.quantize(W)
# X quantized statically on a calibration dataset
int8_quantizer_x = Quantizer(calibration_dataset, bits=8)


for i in range(num_batches):
    X = ...
    if X.dtype == np.float32:
        int_8_X = int8_quantizer_x.quantize(X)
    elif X.dtype == np.int8:
        int_8_X = X
    int_8_results = np.matmul(int_8_X, int_8_W, dtype=np.int32)

Quantization Flow: PTQ vs QAT

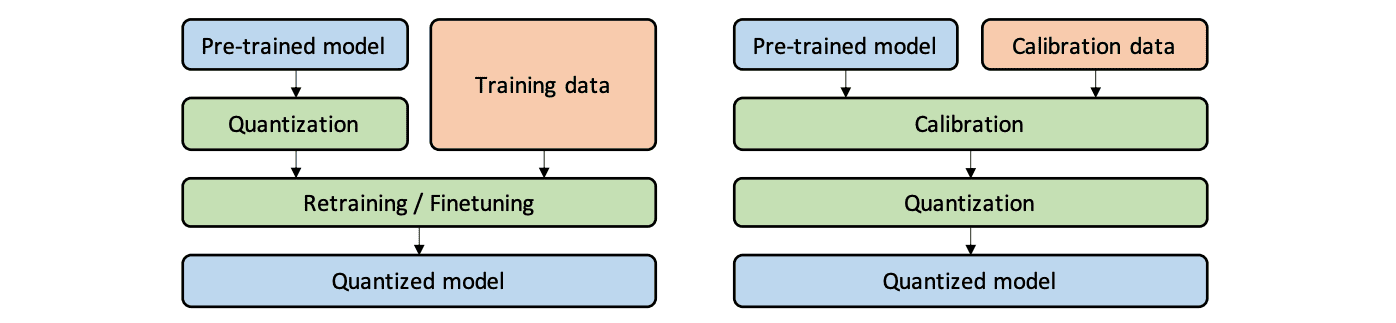
qat_ptq

PTQ (Post Training Quantization) is basically a calibration step after training. It performs calibration with a representative dataset to determine optimal quantization parameters for activations. This is usually done by inserting Observer into the graph to collect tensor statistics like min/max value of the Tensor passing through the observer and then calculate quantization parameters based on the collected tensor statistics.

On the other hand, QAT (Quantization-Aware Training) is done during training. It inserts FakeQuantize modules into the graph so that all weights and activations are “fake quantized” during both the forward and backward passes of training. Float values are rounded to mimic int8 values, but all computations are still done with floating point numbers. Thus, all the weight adjustments during training are made “aware” of the fact that the model will ultimately be quantized; therefore, QAT usually gives higher accuracy than PTQ.

Search